Heap
Is a specialized tree-based data structure which is essentially an almost complete tree that satisfies the heap property: in a max heap, for any given node C, if P is a parent node of C, then the key (the value) of P is greater than or equal to the key of C. In a min heap, the key of P is less than or equal to the key of C. The node at the "top" of the heap (with no parents) is called the root node.
The heap is one maximally efficient implementation of an abstract data type called a priority queue, and in fact, priority queues are often referred to as "heaps", regardless of how they may be implemented. In a heap, the highest (or lowest) priority element is always stored at the root. However, a heap is not a sorted structure; it can be regarded as being partially ordered. A heap is a useful data structure when it is necessary to repeatedly remove the object with the highest (or lowest) priority.
A common implementation of a heap is the binary heap, in which the tree is a binary tree (see figure). The heap data structure, specifically the binary heap, was introduced by J. W. J. Williams in 1964, as a data structure for the heapsort sorting algorithm. Heaps are also crucial in several efficient graph algorithms such as Dijkstra's algorithm. When a heap is a complete binary tree, it has a smallest possible height—a heap with N nodes and for each node a branches always has loga N height. (Source: Wikipedia)
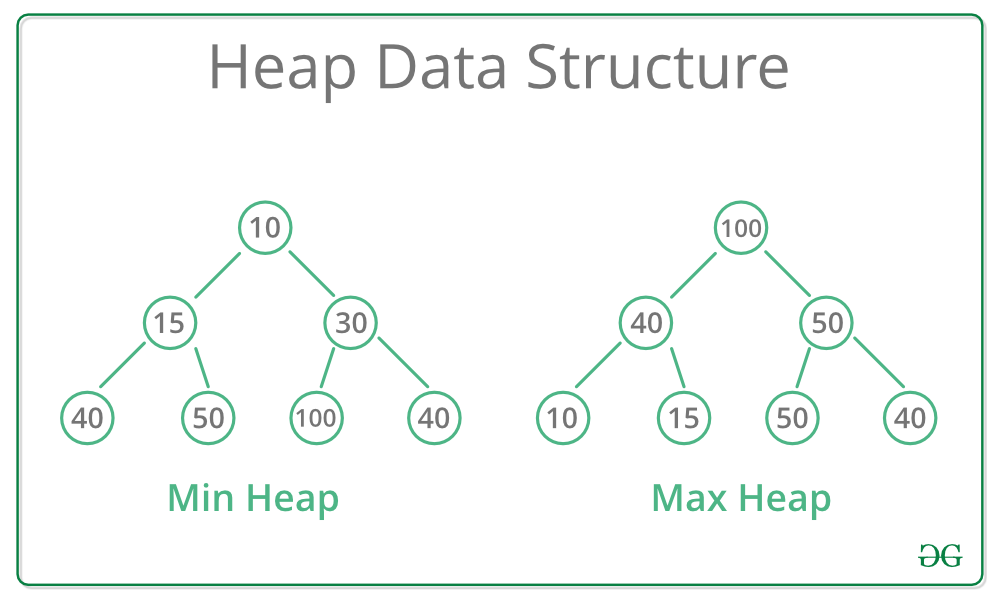
Types of heaps:
There are several different types of heaps, each with a different implementation and various advantages and disadvantages. However, each heap type satisfies the heap property and can be used for the same types of tasks.
| Operation | find-min | delete-min | insert | decrease-key | meld |
|---|---|---|---|---|---|
| Binary | Θ(1) | Θ(log n) | O(log n) | O(log n) | Θ(n) |
| Leftist | Θ(1) | Θ(log n) | Θ(log n) | O(log n) | Θ(log n) |
| Binomial | Θ(1) | Θ(log n) | Θ(1)* | Θ(log n) | O(log n) |
| Fibonacci | Θ(1) | O(log n)* | Θ(1) | Θ(1)* | Θ(1) |
| Pairing | Θ(1) | O(log n)* | Θ(1) | o(log n)* | Θ(1) |
| Brodal | Θ(1) | O(log n) | Θ(1) | Θ(1) | Θ(1) |
| Rank-pairing | Θ(1) | O(log n)* | Θ(1) | Θ(1)* | Θ(1) |
| Strict Fibonacci | Θ(1) | O(log n) | Θ(1) | Θ(1) | Θ(1) |
| 2-3 heap | O(log n) | O(log n)* | O(log n)* | Θ(1) | ? |
* Amortized time