Strongly connected components
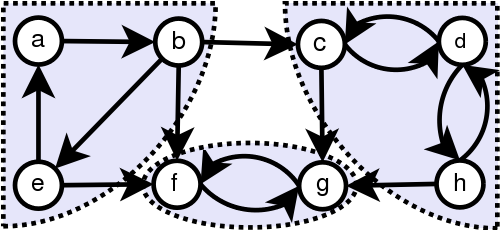
A graph is said to be strongly connected if every vertex is reachable from every other vertex. The strongly connected components of an arbitrary directed graph form a partition into subgraphs that are themselves strongly connected. It is possible to test the strong connectivity of a graph, or to find its strongly connected components, in linear time.
A directed graph is called strongly connected if there is a path in each direction between each pair of vertices of the graph. That is, a path exists from the first vertex in the pair to the second, and another path exists from the second vertex to the first. In a directed graph G that may not itself be strongly connected, a pair of vertices u and v are said to be strongly connected to each other if there is a path in each direction between them. [Source: Wikipedia]
Complexity
| Name | Best time | Space | Comments |
|---|---|---|---|
| Strongly connected components | v + e | v + e |
* Where v = number of visited vertices; e = number of visited edges
* Where b = branching factor of the tree/graph, d = depth of the goal node.